Word Tour: One-dimensional Word Embeddings via the Traveling Salesman Problem

In the field of Natural Language Processing (NLP), a central theme has always been “how to make computers understand the meaning of words.” One fundamental technique for this is “Word Embedding.” This technique converts words into numerical vectors (lists of numbers), with methods like Word2Vec and GloVe being well-known.

Using these vectors allows for calculations like “King – Man + Woman = Queen” and measuring the semantic similarity between words. While a very powerful technique, it has one major characteristic (and sometimes drawback): these vectors are very high-dimensional. For example, commonly used GloVe embeddings use 300 numbers to represent a single word.

While high dimensionality offers the benefit of rich expressive power, it also comes with downsides:

1. High memory consumption (Handling 400,000 words with 300-dimensional GloVe requires about 1GB).
2. Computationally expensive (Requires calculations involving many numbers).
3. Difficult for humans to interpret (Can you imagine a 300-dimensional space?).

Especially when wanting to use NLP on “edge devices” like smartphones or small sensors, this memory usage and computation time become barriers.

We propose “one dimensional word embeddings” to overcome this issue.

You might think it’s impossible to embed words into a line. Indeed, many researchers have believed that capturing word meaning requires at least tens of dimensions.

However, our proposed “Word Tour” tackles this seemingly reckless challenge with a specific approach. In this article, we will explain this surprising idea and its potential.

“Completeness” and “Soundness”: The Key to 1D Embedding

First, let’s organize the properties that an ideal word embedding should satisfy. We broke this down into two aspects: “Completeness” and “Soundness.”

• Completeness: Semantically similar words should be placed close to each other in the embedding space. (e.g., “cat” and “kitten” should be nearby).
• Soundness: Words placed close to each other in the embedding space should actually be semantically similar. (e.g., we don’t want “car” next to “cat”).

Existing high-dimensional embeddings try to satisfy both of these at a high level. However, satisfying both in the extremely constrained space of one dimension is impossible.

So, Word Tour takes a bold paradigm shift: we decided to thoroughly pursue “Soundness,” even if it means sacrificing some Completeness.

What does this mean? Word Tour accepts the possibility that semantically similar words (e.g., “cat” and “pet”) might end up far apart on the 1D line (sacrificing Completeness). But in return, it aims to ensure that words adjacent on the 1D line are semantically close (pursuing Soundness).

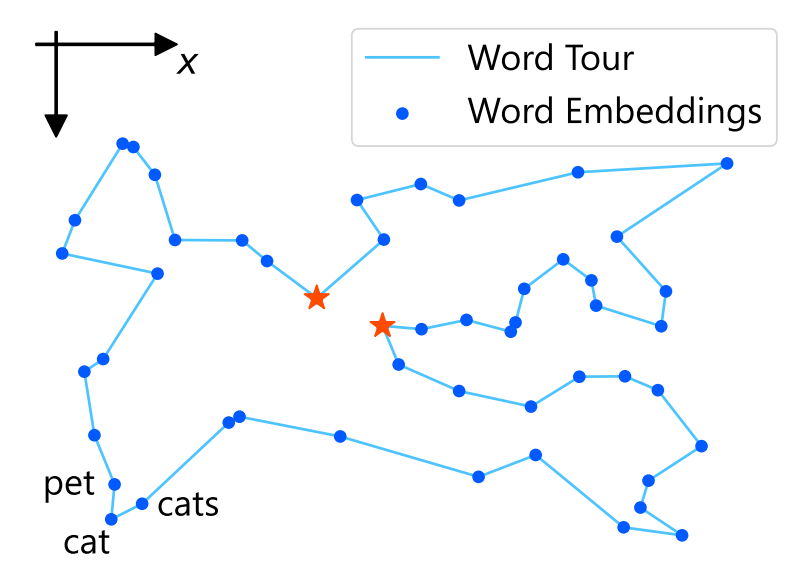
You might wonder, “Isn’t it a problem if similar words are far apart?” Indeed, it might become unsuitable for tasks like word analogy (“King – Man + Woman = ?”). However, the guaranteed “Soundness” offers advantages. For instance, when looking for “paraphrase candidates” for a word, simply looking at its neighbors on the line reliably finds semantically close words. Also, in document retrieval, similar documents found using Word Tour are highly likely to be genuinely relevant in content (though some might be missed due to the completeness trade-off). In other words, while recall might be lower, high precision is guaranteed.

Determining Word Order via the “Traveling Salesman Problem”

So, let’s find the optimal “sequence (order)” of words such that adjacent words are semantically close.

This is where the classic computer science problem, the “Traveling Salesman Problem (TSP)”, comes into play.

In a nutshell, we regard a word as a city and find the best order in this formulation

Let’s think about the condition “adjacent words are semantically close” mathematically. Let \(x_i\) be the vector representing word \(i\) in the original high-dimensional embedding (e.g., GloVe). If we denote the word order as \(\sigma = (\sigma_1, \sigma_2, …, \sigma_n)\), our approach is to minimize the “sum of distances between adjacent words (in the original embedding space).”

$$ \min_{\sigma \in \mathcal{P}([n])} \sum_{i=1}^{n-1} ||x_{\sigma_i} – x_{\sigma_{i+1}}||_2 + ||x_{\sigma_n} – x_{\sigma_1}||_2 $$

• \(\sigma\): The word order (tour)
• \(x_{\sigma_i}\): The vector of the \(i\)-th word in the sequence
• \(||x_a – x_b||_2\): The distance between word \(a\) and word \(b\) (smaller means closer)
• \(\sum\): Sum the distances for all adjacent pairs
• \(\min\): Find the sequence \(\sigma\) that makes the total distance smallest

This formulae says: “Find the route (word order) that visits every word (city) exactly once and returns to the start, such that the total distance traveled (sum of distances between adjacent words) is minimized.” This is precisely the Traveling Salesman Problem! Words correspond to “cities,” and the semantic distance between words corresponds to the “distance between cities.”

NP-hard? But It’s Okay! Techniques for Solving Huge TSPs

TSP belongs to a class of problems called “NP-hard,” where finding the optimal route becomes exponentially more time-consuming as the number of cities (words) increases. The number of words we are dealing with is 40,000. Trying to solve this naively would take astronomical amounts of time.

However, even if theoretically difficult, high-performance TSP solvers exist in practice. We used a particularly powerful LKH solver, which uses an improved version of the Lin-Kernighan algorithm. The advantages of this solver is

1. It can find near-optimal solutions for TSPs with even hundreds of thousands of cities within practical time.
2. It provides a certificate of the (near) optimality using the dual problem.

In fact, when we ran the LKH solver with the 40,000 GloVe vectors as input, the resulting “total adjacent word distance” was guaranteed to be within 1.003 times the theoretical lower bound. In other words, we were able to find an almost perfect “Word Tour.”

The surprising point here is that, contrary to the implication of “NP-hard,” in practical problem-solving, heuristic algorithms and implementation can often solve very large-scale instances efficiently, sometimes even with theoretical guarantees.

Benefits of Word Tour

The 1D word order “Word Tour” obtained this way has attractive properties:

1. Ultra-Lightweight: Word Tour only records the “order” of words. There’s no need to store large amounts of floating-point numbers like in the original high-dimensional vectors. The file size for a 40,000-word Word Tour is just 300KB! This is drastically smaller compared to the original GloVe. This makes it easily runnable even on low-memory devices.
2. Fast: To find out how close word A and word B are, high-dimensional vectors require many numerical calculations. With Word Tour, you just look at the difference in their positions on the line (e.g., if A is 100th and B is 105th, the difference is 5). Finding similar words also just involves looking at a few neighbors before and after the word on the line.
3. Interpretable: Being 1D, it can be directly plotted and visualized on a line. The overall structure can be grasped without information loss. High-dimensional data requires dimensionality reduction techniques like t-SNE for visualization, which inevitably lose information or make it unclear what information is preserved. Word Tour avoids this issue.

Experiments

1. What Does the Order Look Like? (Qualitative Evaluation)

First, let’s look at a part of the actual Word Tour obtained.

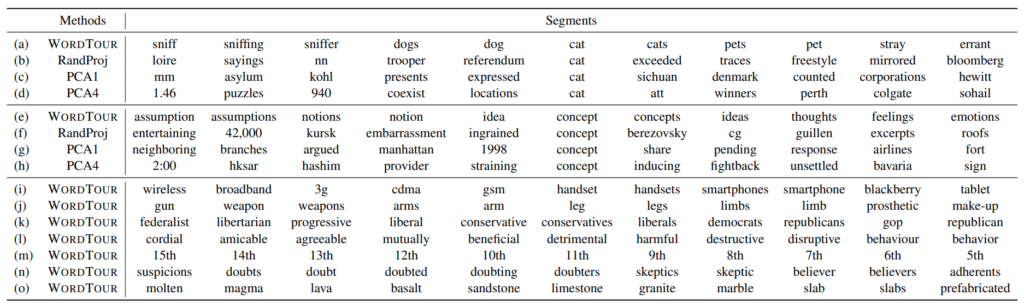
The entire Word Tour can be viewed at https://github.com/joisino/wordtour/blob/main/wordtour.txt. Naturally, a key feature is that this 40,000-line text file is the entire embedding.

2. Does It Align with Human Intuition? (User Evaluation)

Next, we used crowdsourcing (Amazon Mechanical Turk) to evaluate how well Word Tour aligns with human intuition. Participants were shown a target word (e.g., “cat”), its neighbor in Word Tour (e.g., “cats”), and its neighbor from another 1D embedding method (e.g., PCA, neighbor “exceeded”), and asked, “Which neighbor is more similar to the original word (cat)?” Here are the results after repeating this 100 times:

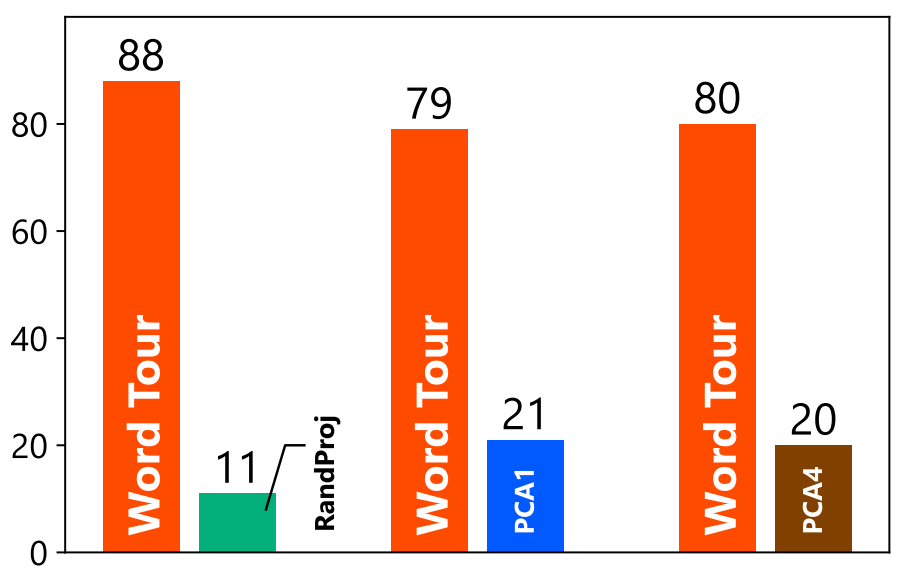
This result indicates that Word Tour is not just numerically optimal but also closely matches human semantic intuition.

3. Is It Useful for Document Classification? (Application Evaluation)

The “Soundness” property of Word Tour (adjacent words are semantically close) can also be applied to document comparison. Standard document comparison methods like “Bag of Words (BoW)” only consider word counts, often failing to capture similarity well because similar words like “cat” and “kitten” are treated as distinct.

Therefore, we propose “Blurred Bag of Words.” This method involves blurring some “weight” to neighbor words on the 1D Word Tour line.

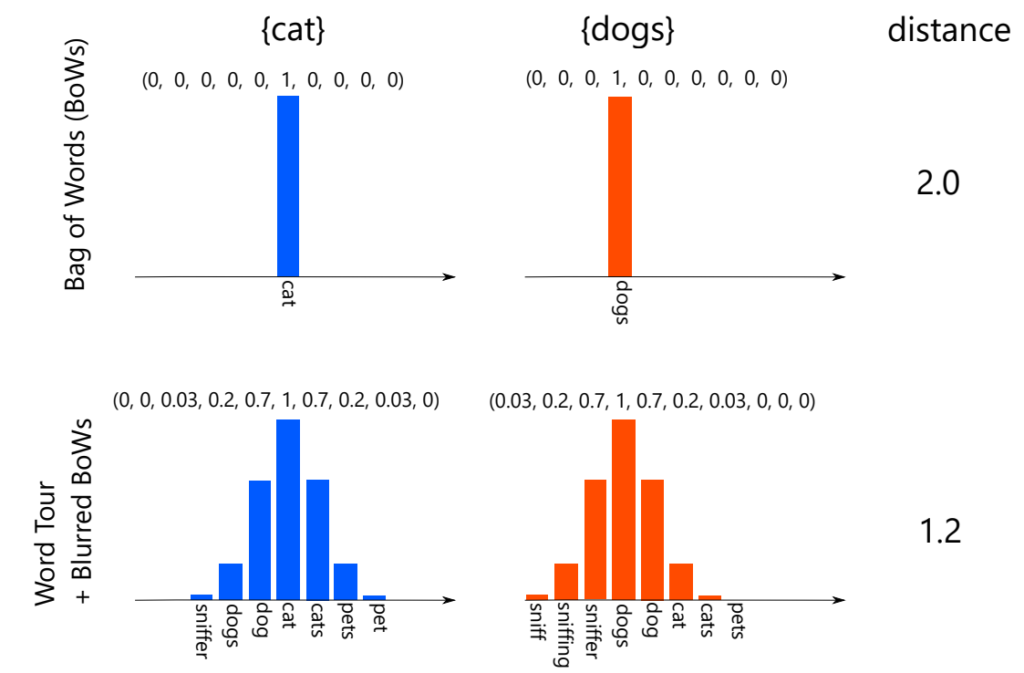
Using this Blurred BoW allows document comparison that considers the influence of nearby similar words on the Word Tour. We evaluated the accuracy of this method on several document classification datasets. We compared it against simple BoW, other 1D methods (RandProj, PCA), and WMD (Word Mover’s Distance), which uses high-dimensional embeddings for high accuracy but is computationally very expensive.

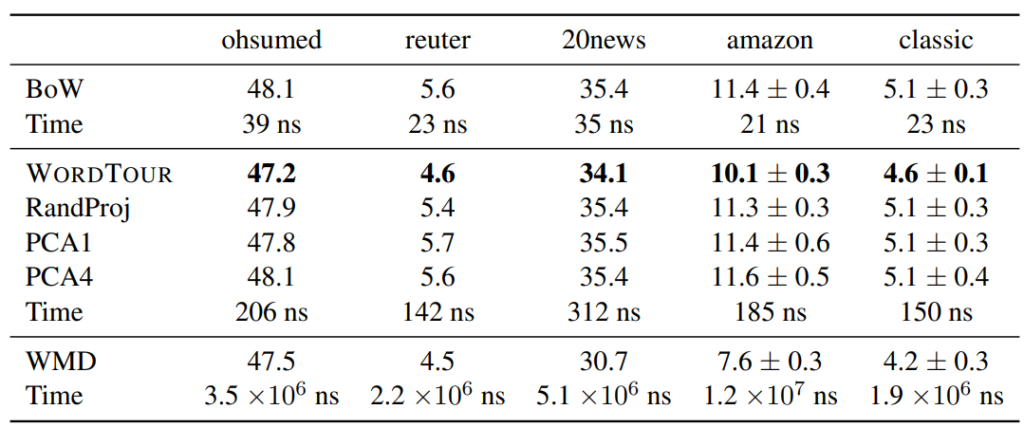
These results suggest that in resource-constrained scenarios (where WMD might be infeasible), Word Tour can be a superior alternative to BoW, offering better accuracy than other 1D methods. It can be described as a well-balanced approach: lightweight and fast, yet still able to consider word similarity.

Conclusion: New Possibilities Opened by Word Tour

The “Word Tour” proposed in this paper is a unique approach that challenges conventional wisdom in word embeddings.

• We decomposed word embedding properties into “Completeness” and “Soundness,” achieving 1D embedding by focusing on “Soundness.”
• We formulated the problem of finding the optimal order as a “Traveling Salesman Problem (TSP)” and successfully obtained near-optimal solutions using high-performance solvers.
• The resulting Word Tour possesses significant advantages not found in traditional high-dimensional embeddings: ultra-lightweight, fast, and interpretable.
• Experiments demonstrated that its ordering aligns with human intuition and is effective in document classification tasks.

Of course, Word Tour is not a silver bullet. Sacrificing “Completeness” means it has tasks it’s not well-suited for. However, in scenarios where memory and computation speed are critical, or where interpretability is required, Word Tour holds the potential to be a powerful new option.

This research was a challenge to capture the complexity of words within a deliberately one-dimensional framework. The fact that a classic problem like TSP can contribute to solving modern NLP challenges is also an interesting discovery.

Future directions could include exploring different distance metrics for the TSP cost function or investigating ways to recover some “Completeness.”

We hope that Word Tour can offer new perspectives and tools for future research and applications in natural language processing.

Paper: Word Tour: One-dimensional Word Embeddings via the Traveling Salesman Problem.
GitHub: https://github.com/joisino/wordtour

Author Profile

If you found this article useful or interesting, I would be delighted if you could share your thoughts on social media.

New posts are announced on @joisino_en (Twitter), so please be sure to follow!